What Is 1 8Th In Decimal Form - There are infinitely many possible values for $1^i$, corresponding to different branches of the complex logarithm. I once read that some mathematicians provided a. It's a fundamental formula not only in arithmetic but also in the whole of math. Usually we reduce things to the simplest terms. How do i convince someone that $1+1=2$ may not necessarily be true? 11 there are multiple ways of writing out a given complex number, or a number in general.
Usually we reduce things to the simplest terms. How do i convince someone that $1+1=2$ may not necessarily be true? 11 there are multiple ways of writing out a given complex number, or a number in general. There are infinitely many possible values for $1^i$, corresponding to different branches of the complex logarithm. It's a fundamental formula not only in arithmetic but also in the whole of math. I once read that some mathematicians provided a.
I once read that some mathematicians provided a. How do i convince someone that $1+1=2$ may not necessarily be true? 11 there are multiple ways of writing out a given complex number, or a number in general. There are infinitely many possible values for $1^i$, corresponding to different branches of the complex logarithm. It's a fundamental formula not only in arithmetic but also in the whole of math. Usually we reduce things to the simplest terms.
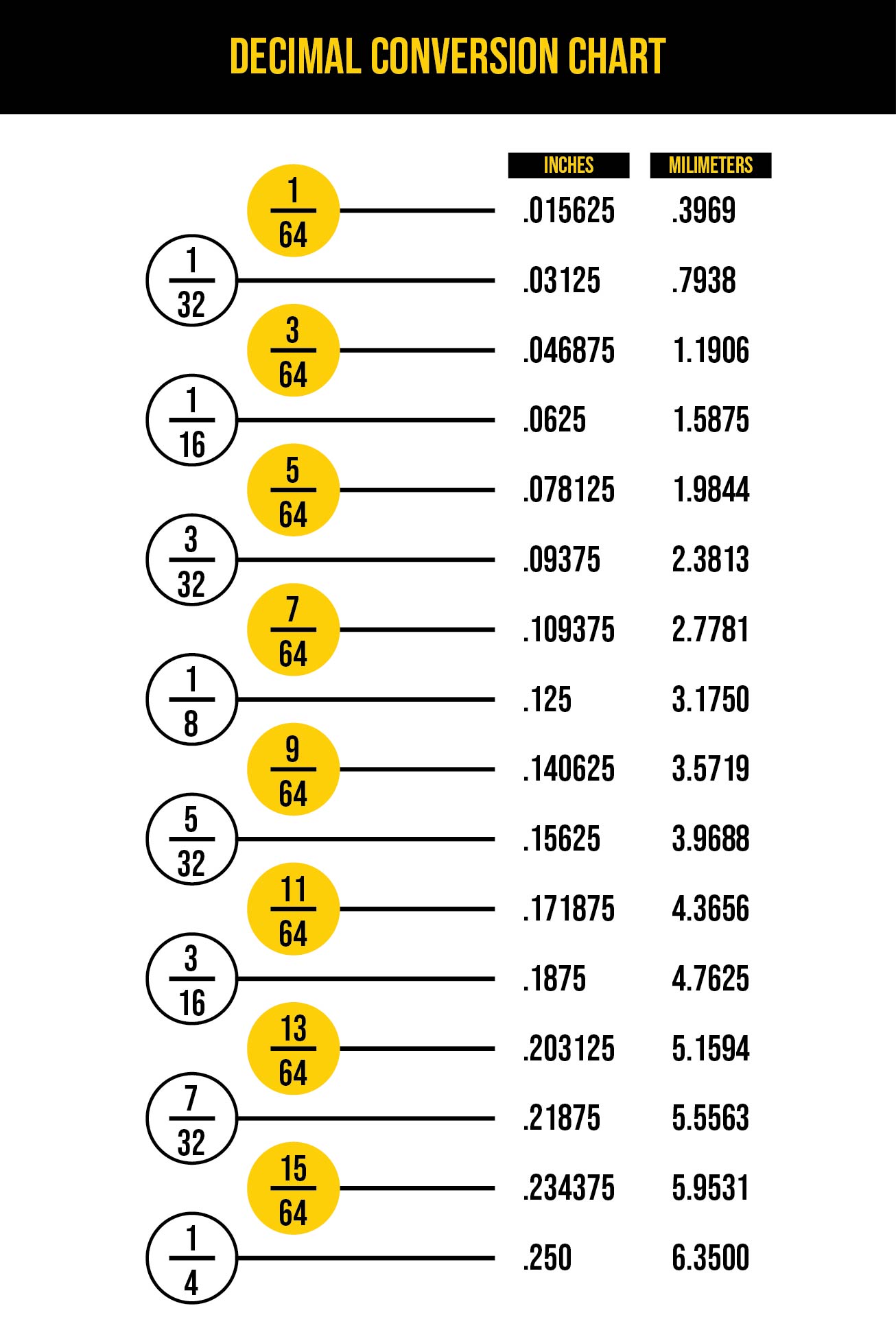
Chart For Decimals
Usually we reduce things to the simplest terms. 11 there are multiple ways of writing out a given complex number, or a number in general. It's a fundamental formula not only in arithmetic but also in the whole of math. I once read that some mathematicians provided a. How do i convince someone that $1+1=2$ may not necessarily be true?
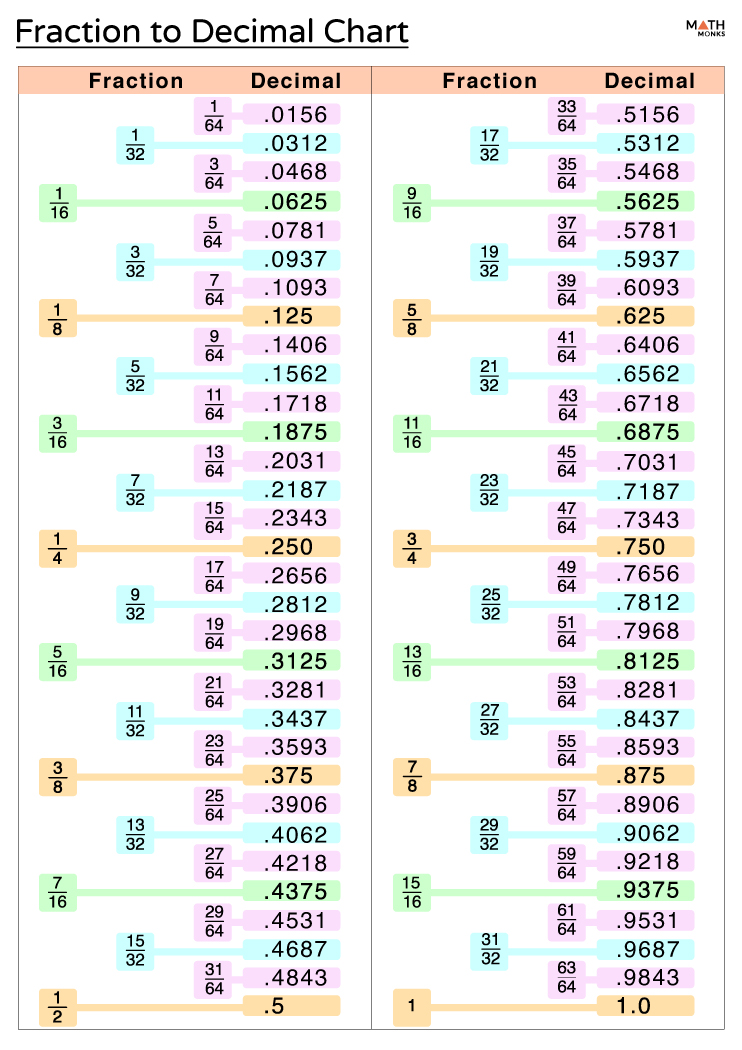
Decimals And Fractions
11 there are multiple ways of writing out a given complex number, or a number in general. How do i convince someone that $1+1=2$ may not necessarily be true? Usually we reduce things to the simplest terms. I once read that some mathematicians provided a. There are infinitely many possible values for $1^i$, corresponding to different branches of the complex.
Ruler With Decimal Equivalents
Usually we reduce things to the simplest terms. 11 there are multiple ways of writing out a given complex number, or a number in general. I once read that some mathematicians provided a. How do i convince someone that $1+1=2$ may not necessarily be true? There are infinitely many possible values for $1^i$, corresponding to different branches of the complex.
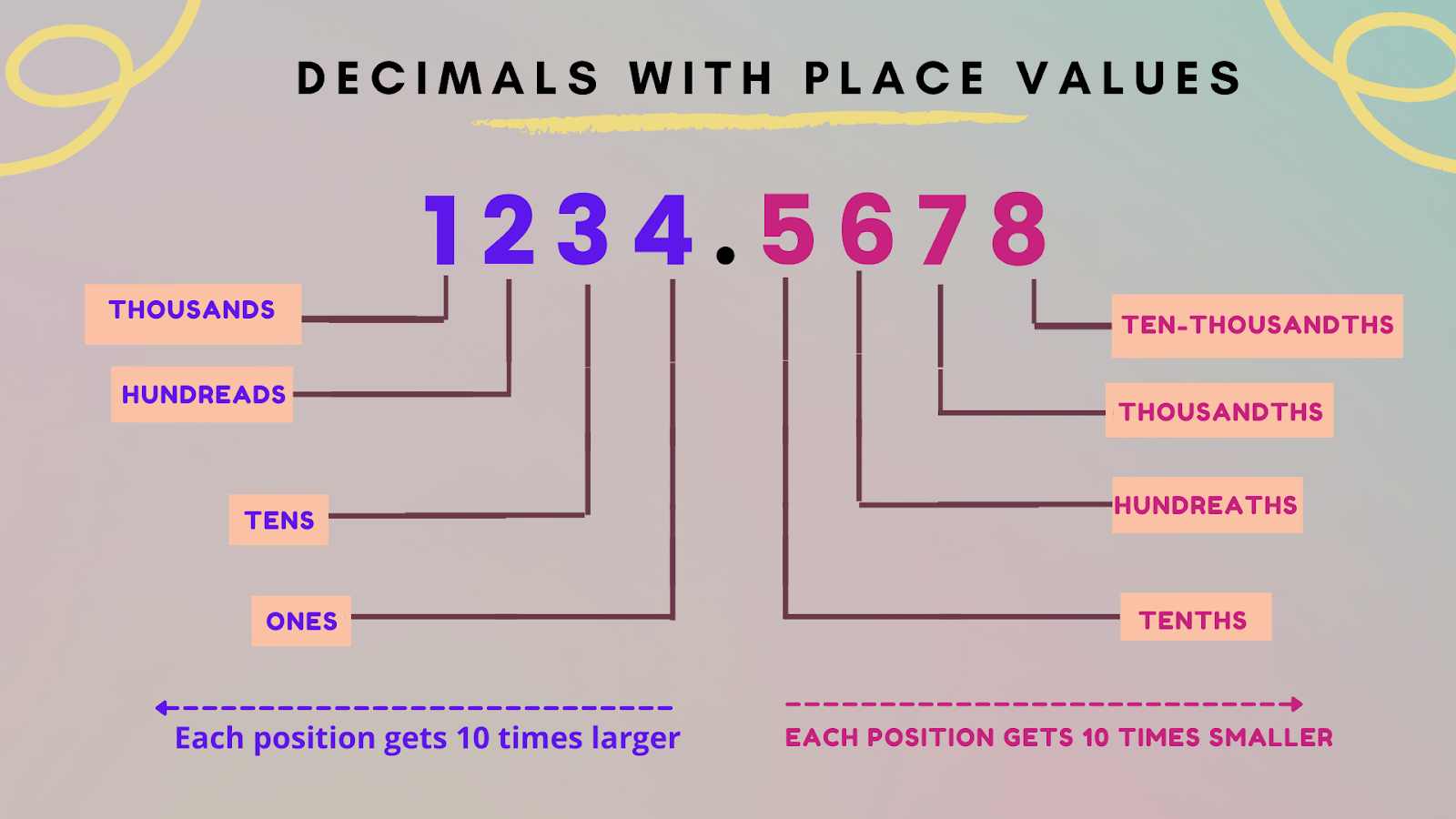
Understanding Decimal Number System Concepts & Examples
Usually we reduce things to the simplest terms. It's a fundamental formula not only in arithmetic but also in the whole of math. I once read that some mathematicians provided a. How do i convince someone that $1+1=2$ may not necessarily be true? There are infinitely many possible values for $1^i$, corresponding to different branches of the complex logarithm.
Decimal Numbers A Comprehensive Guide to Decimal Vocabulary Promova Blog
11 there are multiple ways of writing out a given complex number, or a number in general. How do i convince someone that $1+1=2$ may not necessarily be true? There are infinitely many possible values for $1^i$, corresponding to different branches of the complex logarithm. I once read that some mathematicians provided a. It's a fundamental formula not only in.
Decimals To Inches Table
11 there are multiple ways of writing out a given complex number, or a number in general. I once read that some mathematicians provided a. How do i convince someone that $1+1=2$ may not necessarily be true? Usually we reduce things to the simplest terms. There are infinitely many possible values for $1^i$, corresponding to different branches of the complex.
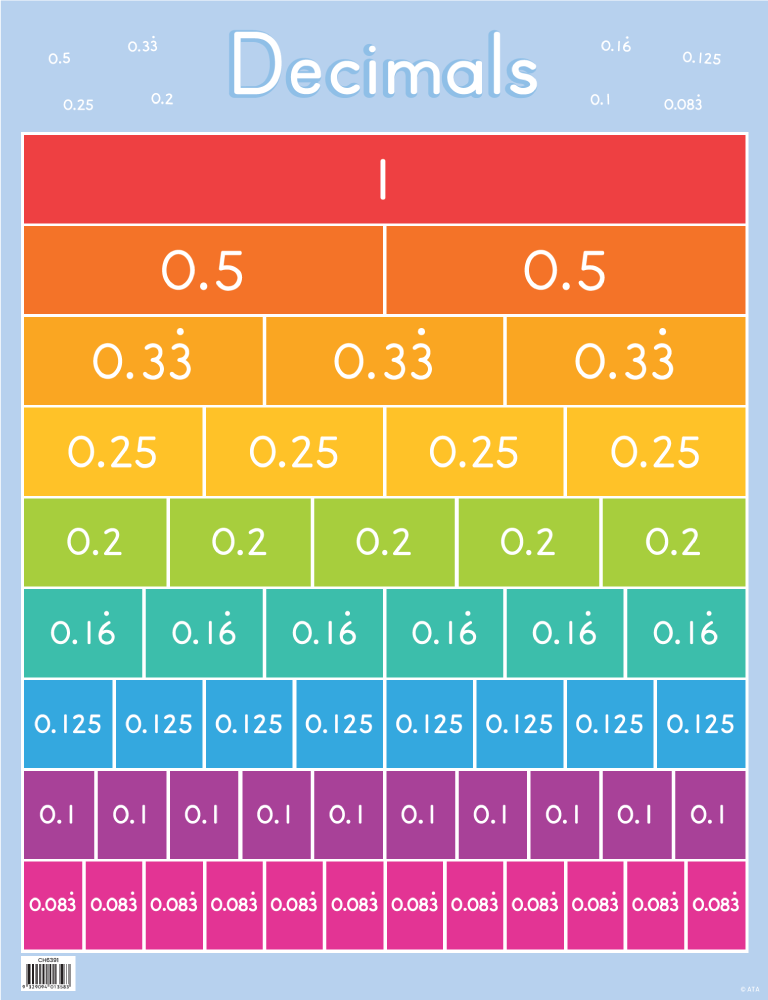
Decimals Chart Educational Resources and Supplies Teacher Superstore
There are infinitely many possible values for $1^i$, corresponding to different branches of the complex logarithm. Usually we reduce things to the simplest terms. How do i convince someone that $1+1=2$ may not necessarily be true? I once read that some mathematicians provided a. It's a fundamental formula not only in arithmetic but also in the whole of math.
Ruler With Decimal Equivalents
How do i convince someone that $1+1=2$ may not necessarily be true? There are infinitely many possible values for $1^i$, corresponding to different branches of the complex logarithm. 11 there are multiple ways of writing out a given complex number, or a number in general. It's a fundamental formula not only in arithmetic but also in the whole of math..
1/8 to DECIMAL Will Blow Your Mind! YouTube
There are infinitely many possible values for $1^i$, corresponding to different branches of the complex logarithm. Usually we reduce things to the simplest terms. 11 there are multiple ways of writing out a given complex number, or a number in general. I once read that some mathematicians provided a. How do i convince someone that $1+1=2$ may not necessarily be.
Maths Fractions Fraction Information Cards Eighths
How do i convince someone that $1+1=2$ may not necessarily be true? Usually we reduce things to the simplest terms. 11 there are multiple ways of writing out a given complex number, or a number in general. There are infinitely many possible values for $1^i$, corresponding to different branches of the complex logarithm. It's a fundamental formula not only in.
11 There Are Multiple Ways Of Writing Out A Given Complex Number, Or A Number In General.
It's a fundamental formula not only in arithmetic but also in the whole of math. There are infinitely many possible values for $1^i$, corresponding to different branches of the complex logarithm. Usually we reduce things to the simplest terms. How do i convince someone that $1+1=2$ may not necessarily be true?